Shear Effects
The effect of shear rate is
normally not a consideration for blending applications. However it can be useful
when blending non-Newtonian fluids, high into a low viscosity fluid or vice
versa. A static mixer can readily handle non-Newtonian fluids, but the shear rate
characteristics needs to be known to calculate the apparent viscosity and hence
the Reynolds number, and the number of mixing elements.
Water treatment applications often request a certain velocity gradient or 'G'
factor. This is actually the average microscale shear rate in the mixer, which
can also be calculated.It should be noted that although all these applications are dependant on
shear, they are in fact all different shear rate.
Non-Newtonian fluids are dependant on the apparent shear rate,High viscosity ratio fluids on the wall shear rate,and water treatment applications on the average microscale shear
rate. These all have different values, so care should be taken to ensure that the
correct figures are used.
Mixing of non-Newtonian fluids is relatively easy in a
Static Mixer. As all the fluid travels through the mixing zones, Static
Mixers get none of the problems associated with cavern formation in agitated
tanks. The only difficulty is calculating the pressure drop, as the viscosity
varies with the shear rate in the mixer. If a graph of shear rate vs viscosity
is obtained from standard tests on a Brookfield viscometer, the apparent shear
rate, can be used to calculate the apparent viscosity.It should be noted that shear vs viscosity tests should be done at
considerably higher pressure shear rates for a Static Mixer than for an agitator
system.The various shear rates associated with Static Mixers as detailed following:
-Wall Shear RateThis is essentially the same as the wall shear rate in a pipe, and is a
function of the fluid velocity.
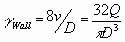
Where v is the pipe velocity, D is the pipe diameter, and Q is the volumetric flowrate. The wall shear rate can be used to ensure that the
additive is drawn off the pipe wall when adding low into high viscosity fluids.
Apparent Shear Rate
The apparent shear rate in the pipe is used to calculate the apparent
viscosity, and hence the pressure drop in non-Newtonian systems. It is basically
a function of the wall shear rate, with a suitable factor added
to take into account the increase in velocity due to the elements causing the
fluid to rotate, and the reduced free area in the pipe. This method of
calculating the apparent shear rate for the mixer is analogous to the Metzner
and Otto shear rate used for calculating apparent viscosities in agitated tank
systems.
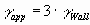
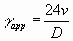
Where g app is the apparent
shear rate, g wall is the wall
shear rate, v is the velocity and D is the pipe diameter.
Average Shear Rate
The average shear rate has fairly recently been given more consideration in
mixer sizing. Essentially it is the same as the velocity gradient used in water
treatment applications, so is a function of the energy usage in terms of
pressure drop through the mixer. The following includes a derivation of the
formula: -The average shear rate is defined as 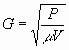 As As 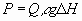 and and 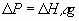 We can say that We can say that 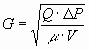
Simplifying for the volume 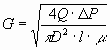
Or 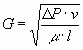
Where G is the average shear rate, P is the power, m is the viscosity, V, D and l are the Mixer volume, diameter
and length respectively, Q is the volumetric flowrate, v is the
velocity and D P is the mixer pressure loss.
Note that the average shear values obtained will be substantially higher than
those usually associated with an agitated tank. Static mixers create uniform
shear distributions, whereas an agitated tank is not. The shear rate is
relatively high, the maximum shear rate is still likely to be substantially
lower than that of an agitated tank. |