Pressure Drop
Three criteria are needed to determine the pressure drop across a static
mixer.
- Reynolds Number - Re
- Pressure drop in an empty pipe of the same length as the Mixer elements.
- A flow coefficient, or friction factor correction factor for the static
mixer.
Reynolds Number can be calculated - See Reynolds # section.
Pressure Drop in an Empty Pipe
For calculation of the pressure drop in an empty pipe, use the standard Darcy
equation, and the Darcy friction factor.
The equation for the pressure drop is as follows:
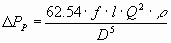
|
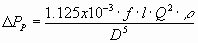
|
Where D PP = pipe pressure drop (kPa) |
Where D PP = pipe pressure drop (psi) |
f = Darcy friction factor |
f = Darcy friction factor |
l = Element length (mm) |
l = Element length (inch) |
Q = Flow rate (m3/h) |
Q = Flow rate (gpm) |
r = Density (kg/m3) |
sg = Specific Gravity |
D = Pipe I.D (mm) |
D = Pipe I.D (inch) |
An estimation of the friction factor can be made from the equations below: -
Re>2000 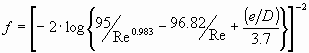
Re<2000 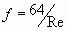
Where e is the surface roughness and D is the pipe diameter in consistent
units.
If this equation were to be used, the recommended value for e would be
0.0457 mm (0.0018 inch).
The flow coefficient is basically a correction factor to compensate for the
increased pressure loss caused by the mixer elements compared with that of an
empty pipe.
The coefficient is given as separate equations for flow regimes.
The following shows the relevant equations for both 1.5:1 and 1:1 pitch
elements.
Flow Condition |
1.5 : 1 Pitch (D<12") |
1 : 1 Pitch (D>=12") |
Re<10 |
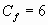
|
|
Re<1000 |
upon request |
|
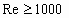
|
upon request |
upon request |
Note that the Pitch is shown as the element length compared with the ID of
the pipe. A 1" element for example would have a 1.5:1 Pitch as standard,
and an ID of 1.049". The element length should therefore be 1.5735".
Also the equations are based on elements of standard thickness. Changes in
either the pitch, or the element width from such things as coatings, will affect
the flow coefficient and therefore the pressure drop.
HENCE,
Static Mixer pressure drop can be calculated by multiplying the standard pipe pressure drop with the flow coefficient.
|